log(sin θ)の不定積分はダイログで書ける
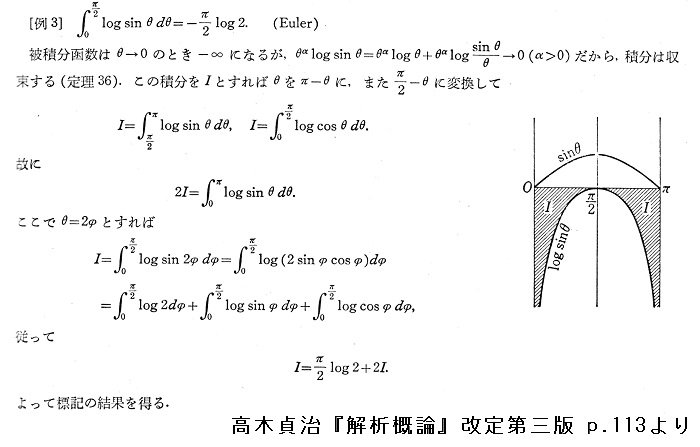
#数楽 添付画像はlog(sin x)の0からπ/2の定積分の計算(高木貞治『解析概論』より)。WolframAlphaを使っていて気づいたのですが、log(sin x)の原始函数はダイログを使って書けるんですね→ http://www.wolframalpha.com/input/?i=\int+log(sin+x)+dx …pic.twitter.com/U0XCu36vPa
#数楽 f(x)=log(sin x)の原始函数はF(x)=(i/2)(x^2 + Li_2(e^(2 i x))) - x log(1 - e^(2 i x)) + x log(sin x) + const.になります。http://www.wolframalpha.com/input/?i=\int+log(sin+x)+dx …
#数楽 Li_2(x)はダイログ(dilogarithm)と呼ばれる函数でLi_2(x)=1/1^2+x/2^2+x^3/3^2+x^4/4^2+…が定義の仕方の一つです。定義より、Li_2(-1)=-Li_2(1)/2となることを容易に示せます(問題:示せ)。
#数楽 Li_2(1)はLi_2(1)=1/1^2+1/2^2+1/3^2+…=ζ(2)と書かれることが多いです。「ζ(2)を求めよ」というのが有名なバーゼル問題です。オイラーが解きました。答えはζ(2)=π^2/6です。
#数楽 『解析概論』p.113に∫_0^{π/2} log(sin x) dx=-(π/2)log 2という公式の示し方が書いてあることをすでに紹介してあります。そして、log(sin x)の原始函数の具体的な表示も紹介した。それらを合わせるとバーゼル問題の解答例が得られます。
#数楽 log(sin x)の「0からπ/2までの定積分の値」と「原始函数の公式」から、(π/2)^2+Li_2(-1)-Li_2(1)=0が得られます。これにLi_2(-1)=-Li_2(1)/2とLi_2(1)=ζ(2)を代入すると、ζ(2)=π^2/6が得られます。
#数楽 『解析概論』にあるように「log(sin x)の0からπ/2までの定積分の値」の計算は易しい。「log(sin x)の原始函数」は答えを知っていれば微分して確認するのは容易です。だから、バーゼル問題の「容易な解答」が一つ得られたことになります。
#数楽 『解析概論』には「log(sin x)の0からπ/2までの定積分の値」の計算には「(Euler)」とあるのでオイラーさんの計算でしょう。オイラーさんは以上で述べたバーゼル問題の解答を知っていたのでしょうかね?
#数楽 「∫_0^{π/2} log(sin x) dx を求めよ」はいかにも大学の微積分の授業で出されそうな問題です。現代の学生は原始函数を求める高校的な方法で問題を解いてしまうかも(WolframAlphaを使えば容易に可能)。ただしζ(2)の値を知らないとダメなんですが。
#数楽 続き。え?ζ(2)の値もWolframAlphaに教えてもらえばいい?それはそうなんですけど、その程度のことなら、WolframAlphaに頼らなくても色々できた方が数学は楽しいです。
#数楽 dilog Li_2(x)程度は「普通の函数」だと思って良さそうですよね。より一般にpolylogがLi_r(x)=x/1^r+x^2/2^r+x^3/3^r+…と定義されることを知っておくのは損ではないと思う。dilogの量子化はとても面白い。
#数楽 ぎょぎょぎょ。『解析概論』p.112には「∫_0^π (x sin x)/(1+(cos x)^2) dx=π^2/4」という公式が書いてあるのですが、その被積分函数の原始函数もdilogを使って表示できるようですね→ http://www.wolframalpha.com/input/?i=\int+(x+sin+x)/(1+(cos+x)^2)+dx …
#数楽 ふうむ。『解析概論』p.112には「∫_0^π (log(1+x))/(1+x^2) dx=(π/8)log 2」という公式も書いてあるのですが、その被積分函数の原始函数もdilogを使って表示できるようです→ http://www.wolframalpha.com/input/?i=\int+(log(1+x))/(1+x^2)+dx …
#数楽 ううむ。『解析概論』pp.112-113の例1~3の定積分の被積分函数はどれもdilog Li_2(x)を用いて表せるのですが、何か一般的な定理があるんですかね?知っている人がいたら教えて下さい。
#数楽 というような感じて、高木貞治『解析概論』のような面白い数学の本を手元において、そこに書いてある式をWolframAlphaに入力するだけで結構遊べますよね。WolframAlphaはiPhoneやAndroid携帯では有料アプリを入れて使うと便利です。
#数楽 現代においては、高木貞治『解析概論』は「証明が書いてある本」としての価値は下がっていると思います。しかし、『解析概論』は面白い式(遊べる式)をたくさん扱っており、楽しめる本としての価値は全く損なわれていないと思います。こういう本は面白いので末永く生き残ることになる。
#数楽 高木貞治『解析概論』を参照するたびに、そこで扱われているネタを保ったまま全部書き直したい気分になるのはどうしてなのだろうか?扱っているネタを減らさないようにすると作業量が膨大になることは明らかなのでやらないのですが。主に証明が並んでいる微積分の本はつまらないと思う。
#数楽 @Paul_Painleve ああ、なるほど、x log(sin x)の原始函数はtrilogで表示できますね→ http://www.wolframalpha.com/input/?i=\int+x+log(sin+x)+dx …https://twitter.com/Paul_Painleve/status/820922235330269184 …
#数楽 問題:非負の整数nに対して、x^n log(sin x)の原始函数をpolylogたちで表示できることを示せ。http://www.wolframalpha.com/input/?i=\int+x^4+log(sin+x)+dx …
先日、オイラーの元ネタについてツイートしたばかりですhttps://twitter.com/Paul_Painleve/status/820921168664215552 …

#数楽 不定積分 ⌠ log(sin x) dx などが多重対数で書けること。添付画像は WolframAlpha で計算した結果。pic.twitter.com/YSvwnwAsaQ

#数楽 log(1+x)/(1+x^2) や (x sin x)/(1+cos^2 x) の不定積分もダイログを使って表せる。添付画像はWolframAlphaを使って計算した結果。pic.twitter.com/gXjcNX1v2s
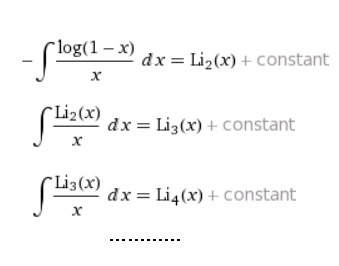

#数楽 f_r(z)=Li_r(e^z)=(r重のポリログにe^zを代入したもの、Li_1(x)=-log(1-x))とおくと、⌠ f_r(z) dz = f_{r+1}(z) + const.pic.twitter.com/Ei1Edu2B1f
#数楽 続き。sin x=(e^{ix}-e^{-ix})/(2i)なので⌠log(sin x)dxの計算は公式-⌠log(1-e^z)dz=Li_2(z)+const.に帰着します。これがlog(sin x)の不定積分にダイログが出て来る理由です。
#数楽 f_{r+1}の導函数がf_rのとき部分積分の繰り返しによって、⌠z^n f_r(z)dz=z^n f_{r+1}(z)-nz^{n-1}f_{r+2}(z)+…+(-1)^n n! f_{r+n+1}(z).これをf_1(z)=-log(1-e^z)に~続く
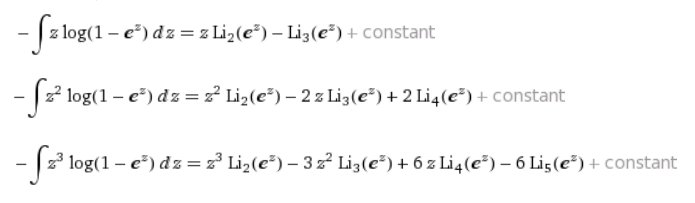
#数楽 続き~適用すれば、f_r(z)=Li_r(e^z)なので、-⌠z^n log(1-e^z)dz=z^n Li_2(e^z)-nz^{n-1}Li_3(e^z)+…+(-1)^n n! Li_{n+2}(e^z).pic.twitter.com/JEQoOS7JaO
#数楽 というわけで、x^n log(sin x)の不定積分がポリログで書けることはポリログの定義から即導かれる自明なことでした。式が複雑になるのは sin x と 1-e^z の違いが原因。
#数楽 x^n log(sin x)の不定積分にポリログが出て来ることは、多重対数函数Li_r(x)の記号法を使っていたり、複素函数としてのlogやexpを扱っている分だけ「高々高校レベル」とは言えなくなっていますが、「高々高校レベル+ε」程度の難易度のほぼ自明な話でした。
#数楽 ポリログLi_r(x)の定義はLi_r(x)=Σ_{k=1}^∞ x^k/k^r (を解析接続したもの)です。r=0なら等比級数Li_0(x)=x+x^2+x^3+…=x/(1-x)で、r=1ならLi_1(x)=-log(1-x)で本質的に対数。続く
#数楽 続き。x^k/k^r をxで割って不定積分すれば x^k/k^{r+1} になるので、⌠_0^x Li_r(x)/x dx=Li_{r+1}(x)です。「高々高校レベル」とは言えない記号法が得て来ていますが、modulo iikagenで高校レベルの話。続く
#数楽 続き。この連続ツイートを読んでしまうような高校生なら、ポリログの素朴な定義をこれで知ることができたと思う。ポリログのx=1での特殊値はEuler-Riemannのゼータ函数の正の整数rでの特殊値ζ(r)に一致します(自明)。例えばLi_2(1)=ζ(2)=π^2/6。


#数楽 続き。添付画像は https://twitter.com/Paul_Painleve/status/820921168664215552 … で教えてもらった情報。Eulerさんがどのようにlog(sin x)の積分を考えたか。pic.twitter.com/fEsMdPqpZX

#数楽 続き。添付画像は https://twitter.com/Paul_Painleve/status/820922235330269184 … で教えてもらった情報。Eulerさんがどのようにx log(sin x)の積分を扱ったか。pic.twitter.com/cgDgJwkWlI
#数楽 Euler Archive への直接リンクhttp://eulerarchive.maa.org/pages/E393.html http://eulerarchive.maa.org/pages/E432.html
#数楽 このツイートが繋がる返答連鎖の話は、「⌠ log(sin x) dx は本質的にダイログで、⌠ x log(sin x) dx は本質的にトリログなので、それらの特殊値はζ(2)、ζ(3)と関係する」とまとめることができます。

#数楽 ここで、log(sin x)の原始函数のダイログによる表示とΣ1/n^2=π^2/6の関係について訂正しておきたいと思います。log(sin x)の原始函数のダイログによる表示*だけ*から⌠_0^{π/2}log(sin x)dxとΣ1/n^2の値がわかります。続くpic.twitter.com/jpM6SdLjNs
#数楽 続き。log(sin x)の原始函数の公式F(x)=(略)はF(x)を微分すれば正しさを確認できます。そしてF(π/2)-F(0)の実部から⌠_0^{π /2}log(sin x)dxの値が得られ、(虚部)=0からΣ1/n^2=π^2/6が得られます。超簡単。続く

#数楽 続き。x log(sin x)の原始函数をダイログとトリログで表わす公式からはEuler全集E432§21にある公式が得られます。Eulerさんがどんな感じの世界を見ていたかが少しわかった気分になりました。やはり、原始函数の明示的な公式があるなら書き下しておいた方がよい!pic.twitter.com/ywVFaiUcoW

#数楽 続き。x^2 log(sin x)で同様のことをやると、実部から⌠_0^{π/2} log(sin x)dx=(3π/16)ζ(3)-(π3/24)log 2が得られ、虚部=0からζ(4)=π^4/90の独立な証明が得られます。pic.twitter.com/eNtkTF4Szr
#数楽 https://twitter.com/genkuroki/status/845586032598773760 …訂正:リンク先の添付画像中のAlframはWolframが正しい。
#数楽 毎日使っているWolframAlphahttp://www.wolframalpha.com/ 適当にTeXっぽい書き方で数式を入力すると関連の数学的情報を教えてくれます。相当に便利です。iPhoneにも有料アプリを入れて使っている。

#数楽 添付画像はWolframAlphaに教えてもらった log(sin x) の原始函数F(x)が実際に原始函数であることの証明。微分するだけなのですが、初心者はそこでつまるかもしれないので、念のためにノートの画像を公開。pic.twitter.com/z2JnhA8Ysh
#数楽 自明な訂正。リンク先の左辺の⌠_0^{π/2} log(sin x)dxはもちろん正しくは⌠_0^{π/2} x^2 log(sin x)dxです。x^2を書き忘れた。いつもごめんなさい。https://twitter.com/genkuroki/status/845613007212240896 …
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …



